Cheatsheet
Index
- Polynomials
- Exponents and Logarithms
- Trigonometric Formulas
- Function Manipulations
- Limits and Derivatives
Polynomials
Quadratics
Quadratic Formula $$ ax^2 + bx + c = 0$$ $$ x = \frac{-b \pm \sqrt{b^2-4ac}}{2a} $$ Factoring real roots (easy) $$\begin{aligned} x^2 + 2px + p^2 &= (x+p)^2 \\ x^2 - 2px + p^2 &= (x-p)^2 \\ x^2-p^2 &= (x+p)(x-p) \\ x^2 + (p+q)x + pq &= (x+p)(x+q) \\ x^2 + (p-q)x - pq &= (x+p)(x-q) \\ x^2 - (p+q)x + pq &= (x-p)(x-q) \\ \end{aligned}$$ Factoring real roots (advanced) $$\begin{aligned} abx^2 + (aq+bp)x + pq &= (ax+p)(bx+q) \\ x^2 + 2px + p^2 - r^2 &= (x+p+r)(x+p-r) \\ \end{aligned}$$ Factoring complex roots $$\begin{aligned} x^2+b^2 &= (x+bi)(x-bi) \\ x^2+2zx+z^2+b^2 &= (x+z+bi)(x+z-bi) \\ \end{aligned}$$
Cubics
Factoring real roots (easy)
$$\begin{aligned}
x^3+k^3 &= (x+k)(x^2-kx+k^2) \\
x^3-k^3 &= (x-k)(x^2+kx+k^2) \\
\end{aligned}$$
Factoring real roots (advanced)
$$\begin{aligned}
x^3+k_2x^2+k_1x+k_0 &= (x+a)(x^2+bx+c) \\
&= x(x^2+bx+c) + a(x^2+bx+c) \\
&= x^3+bx^2+ax^2+cx+abx+ac
\end{aligned}$$
$$\begin{aligned}
ac &= k_0 \\
ab+c &= k_1 \\
a+b &= k_2
\end{aligned}$$
Exponents and Logarithms
Definition $$\begin{aligned} ln(x) &= log_e(x) && ln(e) = 1 \\ ln(e^x) &= x && e^{ln(x)} = x \\ \end{aligned}$$ Properties $$\begin{aligned} e^0 &= 1 && ln(1) = 0 \\ e^x e^y &= e^{x+y} && ln(xy) = ln(x) + ln(y) \\ \frac{e^x}{e^y} &= e^{x-y} && ln(\frac{x}{y}) = ln(x) - ln(y) \\ (e^x)^y &= e^{xy} && ln(x^y) = y \text{ } ln(x) \\ \end{aligned}$$
Trigonometric Formulas
Basic Formulas
Symmetry $$\begin{aligned} sin(-\theta) &= -sin(\theta) \\ cos(-\theta) &= cos(\theta) \\ tan(-\theta) &= -tan(\theta) \\ \end{aligned}$$ Periodicity $$\begin{aligned} sin(\theta) &= sin(\pi - \theta) = sin(2\pi + \theta) \\ cos(\theta) &= cos(2\pi - \theta) = cos(2\pi + \theta) \\ tan(\theta) &= tan(\pi + \theta) \\ \end{aligned}$$ Relation between functions $$\begin{aligned} tan(\theta) &= \frac{sin(\theta)}{cos(\theta)} \\ sin(\theta) &= cos(\frac{\pi}{2} - \theta) \\ cos(\theta) &= sin(\frac{\pi}{2} - \theta) \\ \end{aligned}$$ Other Identities $$\begin{aligned} & sin^2(\theta) + cos^2(\theta) = 1 \\ & sin(\alpha + \beta) = sin(\alpha)cos(\beta) + cos(\alpha)sin(\beta) \\ \end{aligned}$$
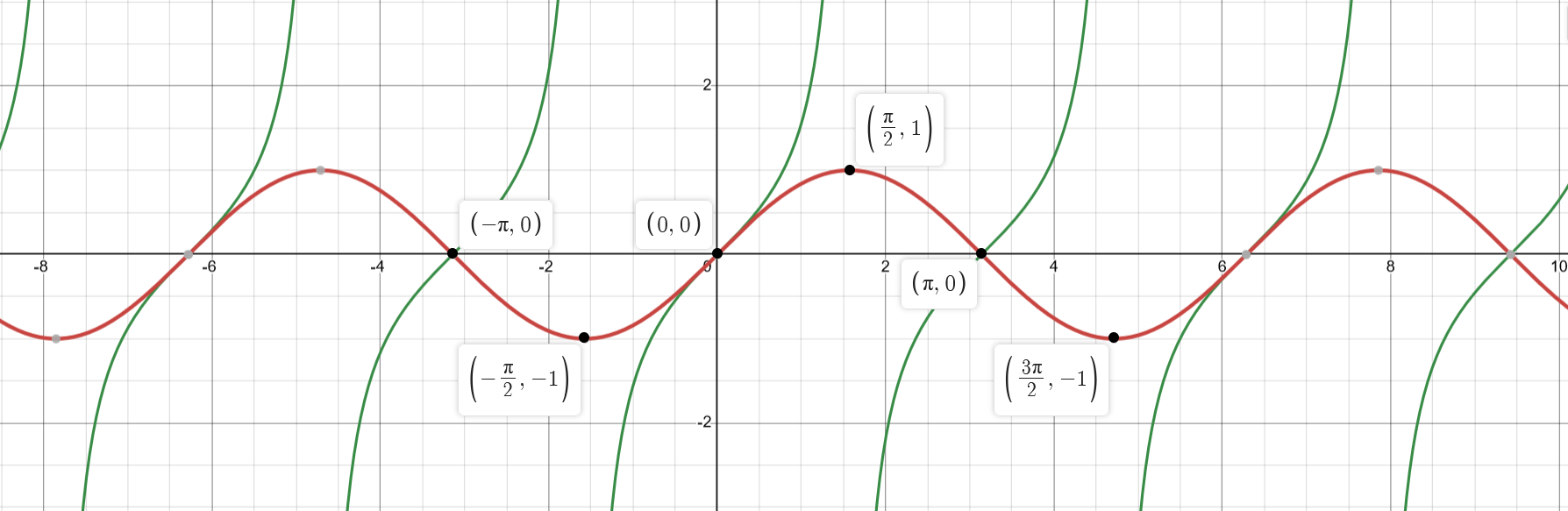
Basic Plots
Unit circle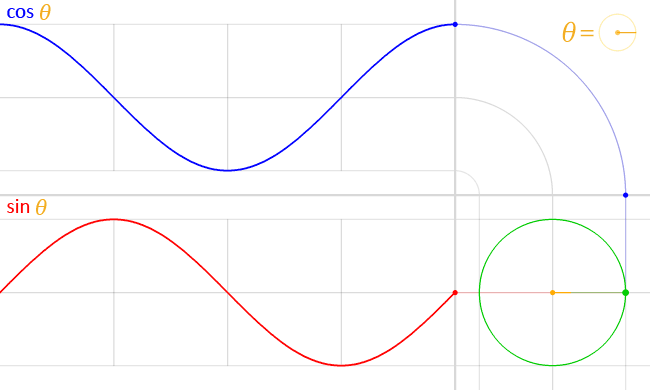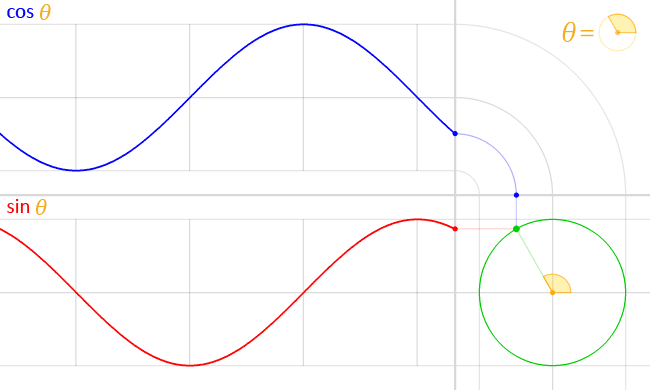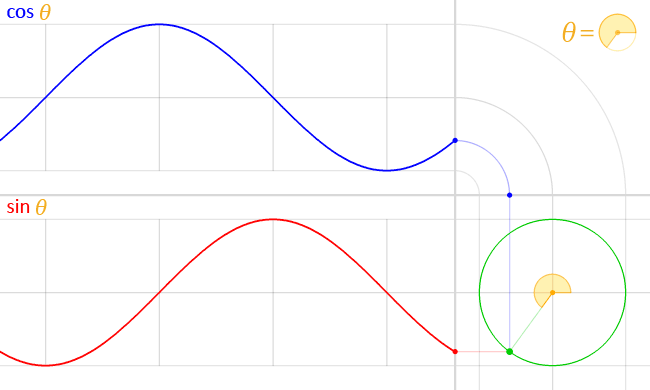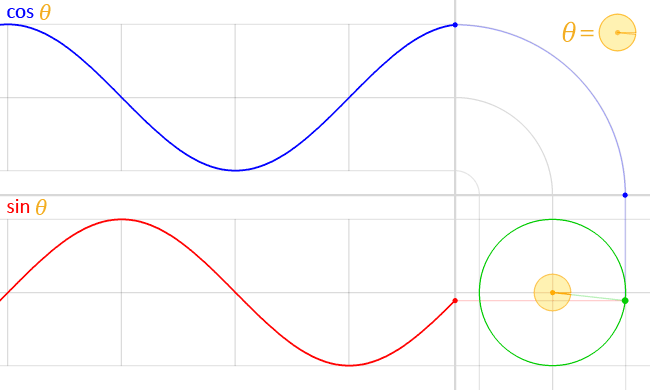
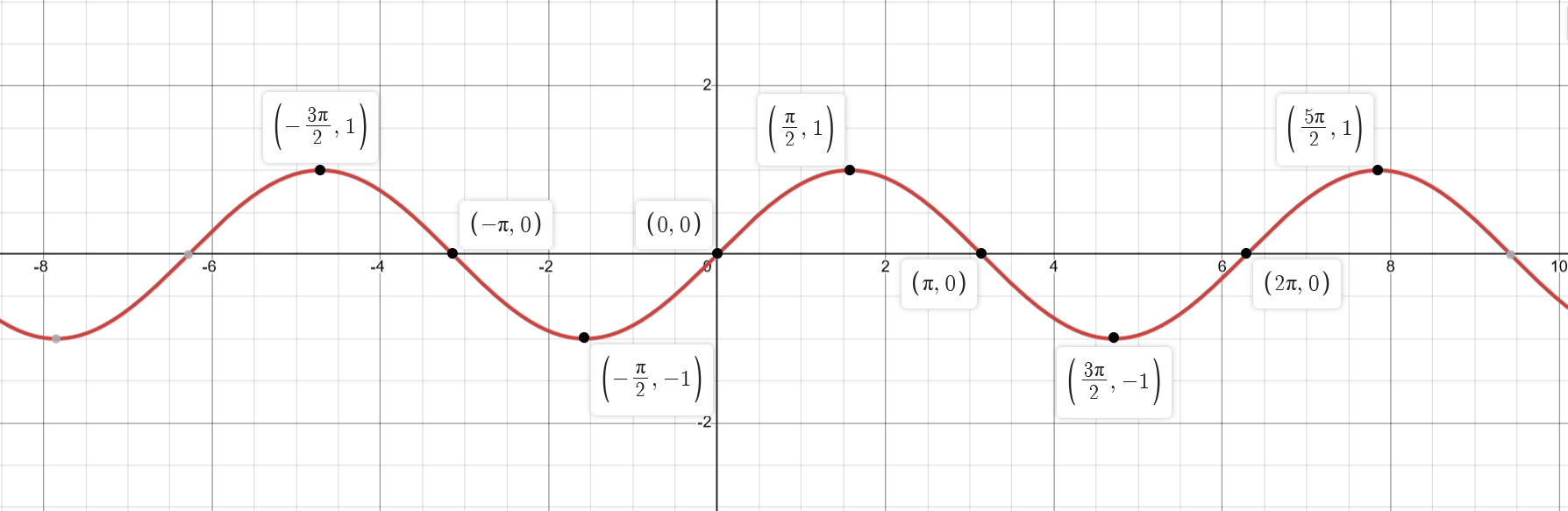
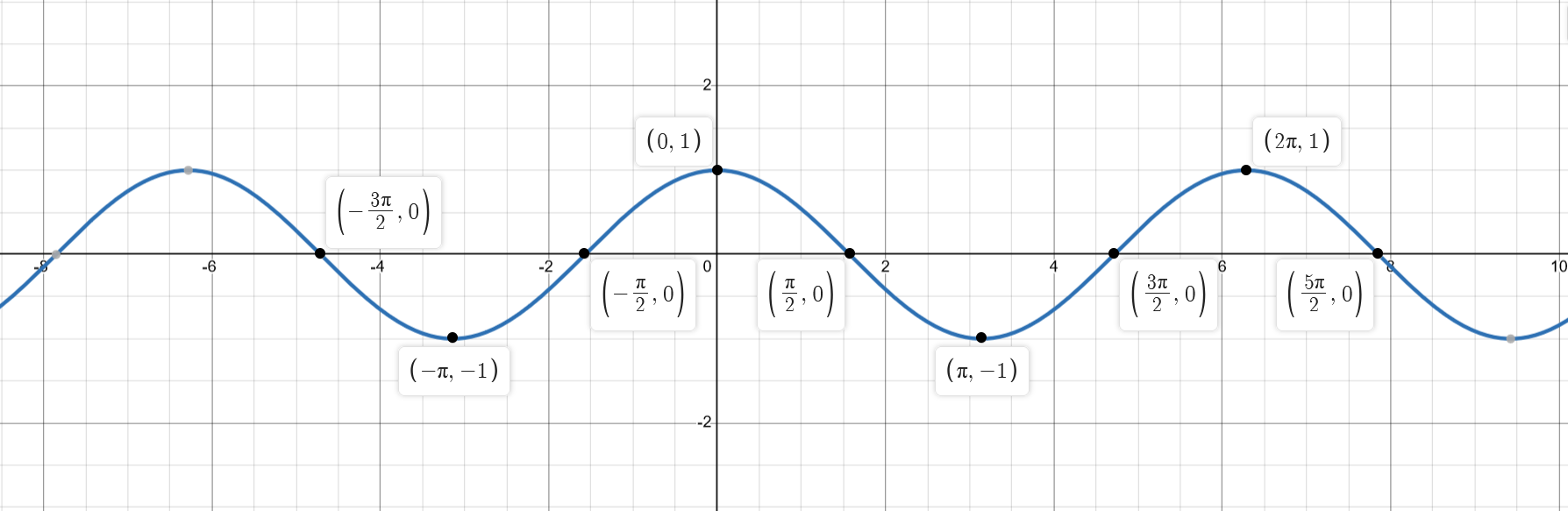
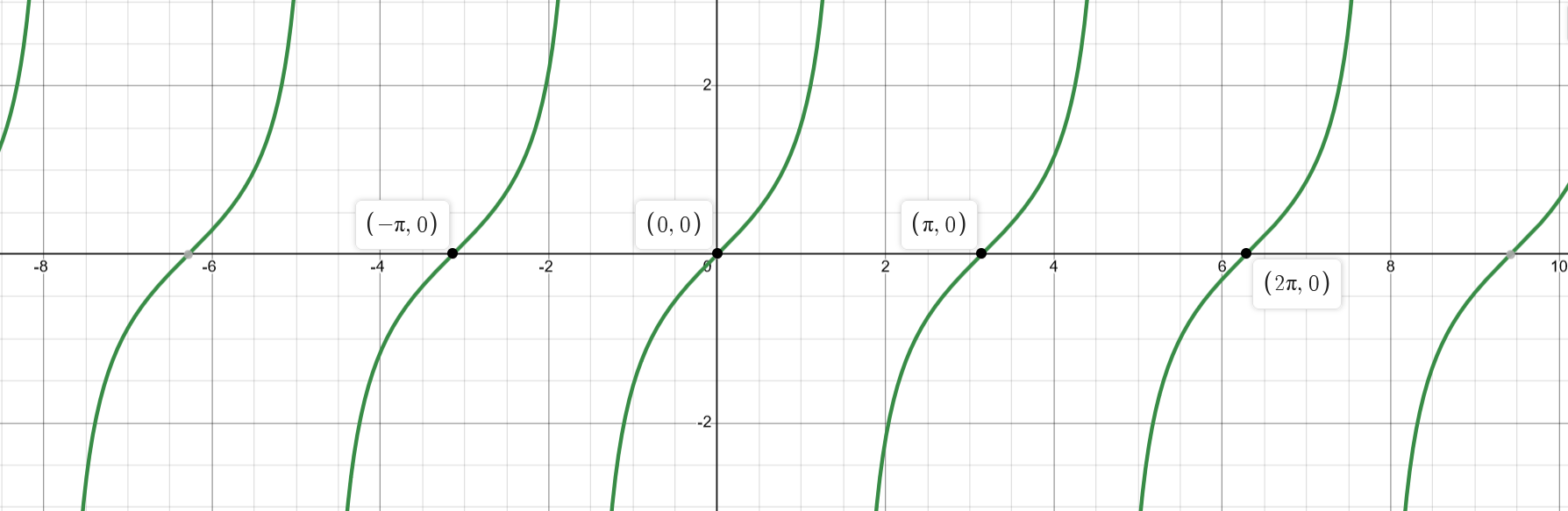
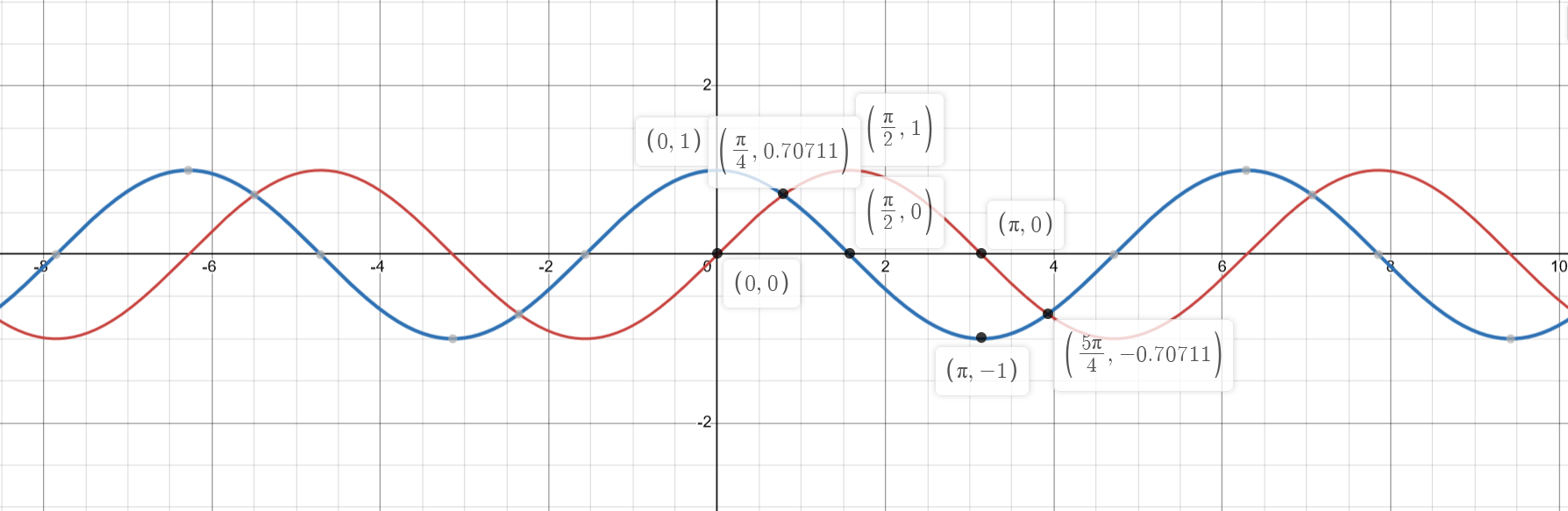
Function Manipulations
One can perform basic manipulations on a function $f(x) = y$ into a new function $g(x)$ with the same "shape" but shifted or scaled along the cartesian plane.
Shifting along $y$
Add a constant $k$ to the function $f$ to shift it along the y-axis: $g(x) = k + f(x)$. Given a point $x_0$ in the x-axis:
$$\begin{aligned}
f(x_0) &= y_0 \\
g(x_0) &= y_1 = k + f(x_0) = k + y_0 \\
y_1 &= y_0 + k \\
\end{aligned}$$
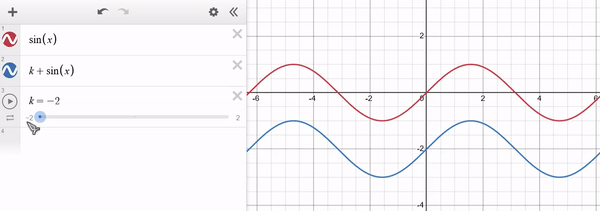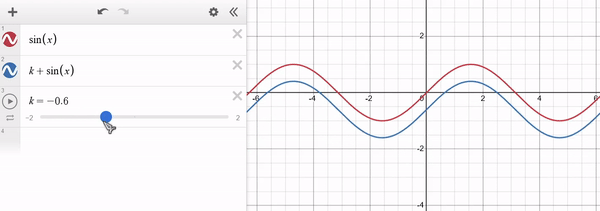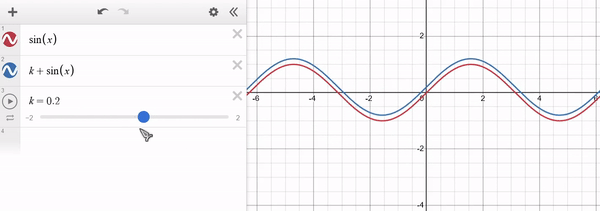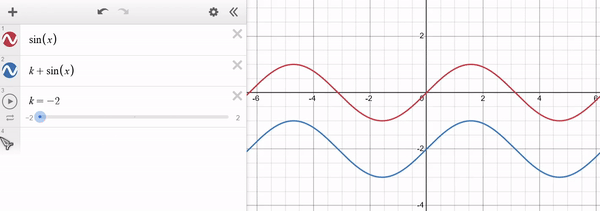
Note that for $k > 0$ the function is shifted towards higher values of $y$ (i.e. upwards) and for $k < 0$ it shifts towards lower values of $y$ (i.e. downwards). The x-axis remains unaffected. Example of $f(x) = sin(x)$ in red and $g(x) = k + sin(x)$ in blue:
Scaling along $y$
Multiply the function $f$ with a constant $k$ to scale it along the y-axis: $g(x) = k*f(x)$. Given a point $x_0$ in the x-axis:
$$\begin{aligned}
f(x_0) &= y_0 \\
g(x_0) &= y_1 = k * f(x_0) = k * y_0 \\
y_1 &= y_0 * k \\
\end{aligned}$$
Note that for $k > 1$ the function "stretches" along $y$ and for $0 < k < 1$ the function "shrinks" along $y$. For $k < 0$ a similar behaviour occurs, with the function being "inverted" along $y$. The x-axis remains unaffected. Example of $f(x) = sin(x)$ in red and $g(x) = k * sin(x)$ in blue:
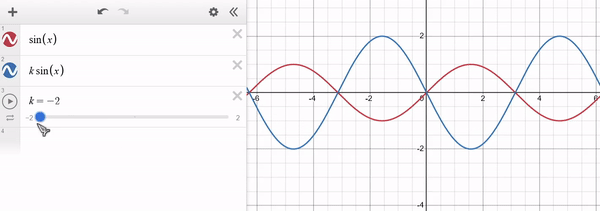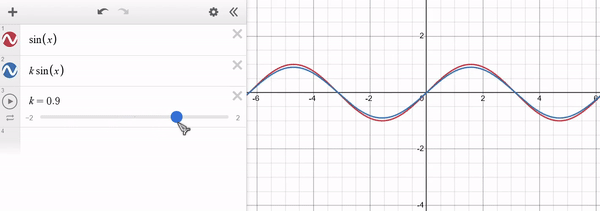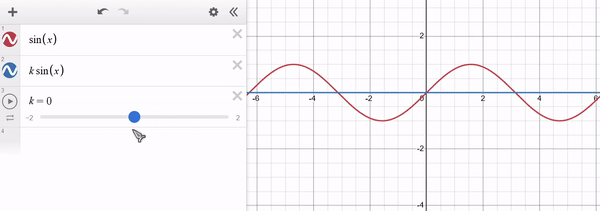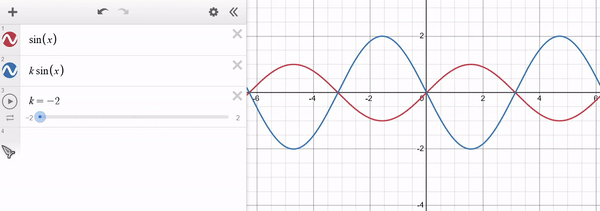
Shifting along $x$
Add a constant $k$ to the argument of the function $f$ to shift it along the x-axis: $g(x) = f(x + k)$. Given a point $x_0$ in the x-axis and its shifted counterpart $x_1 = x_0 - k$:
$$\begin{aligned}
g(x_1) &= f(x_1 + k) = f(x_0 - k + k) \\
g(x_1) &= f(x_0) \\
\end{aligned}$$
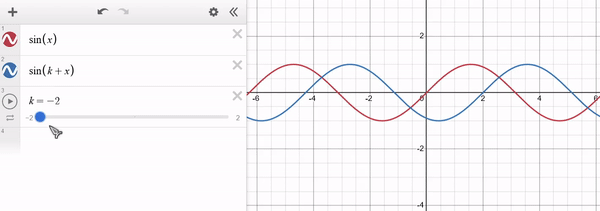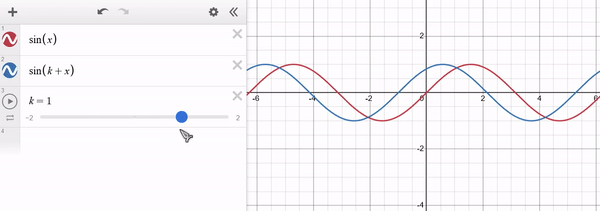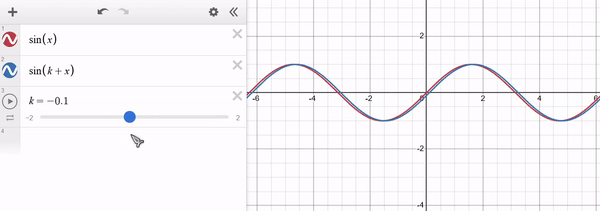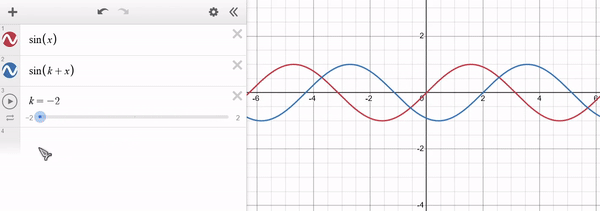
Note that for $k > 0$ the function is shifted towards lower values of $x$ (i.e. to the left) and for $k < 0$ it shifts towards higher values of $x$ (i.e. to the right). The y-axis remains unaffected. Example of $f(x) = sin(x)$ in red and $g(x) = sin(x + k)$ in blue:
Scaling along $x$
Multiply the argument of the function $f$ with a constant $k$ to scale it along the x-axis: $g(x) = f(k*x)$. Given a point $x_0$ in the x-axis its shifted counterpart $x_1 = \frac{1}{k} x_0$:
$$\begin{aligned}
g(x_1) &= f(k x_1) = f(k \frac{1}{k} x_0) \\
g(x_1) &= f(x_0) \\
\end{aligned}$$
Note that for $k > 1$ the function "shrinks" along $x$ and for $0 < k < 1$ the function "stretches" along $x$. For $k < 0$ a similar behaviour occurs, with the function being "inverted" along $x$. The y-axis remains unaffected. Example of $f(x) = sin(x)$ in red and $g(x) = sin(x * k)$ in blue:
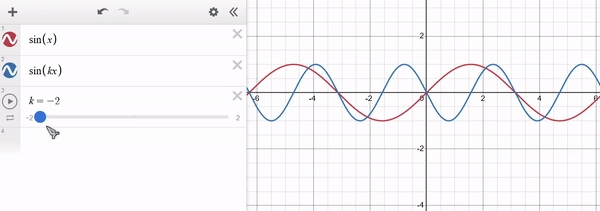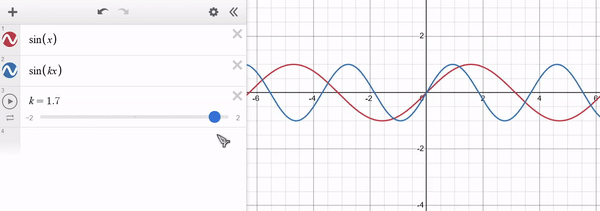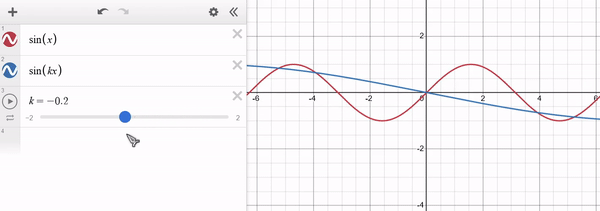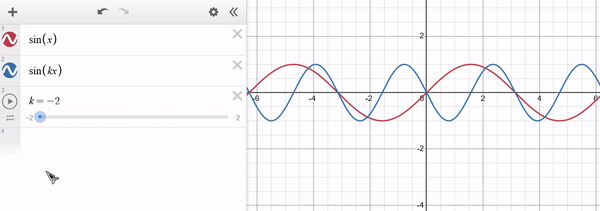
Limits and Derivatives
Speed of Growing Functions
$$\begin{aligned} \lim_{x\to\infty} f(x) = \infty && \lim_{x\to\infty} g(x) = \infty \\ \end{aligned}$$ $$\begin{aligned} \lim_{x\to\infty} \frac{f(x)}{g(x)} &= \infty && \text{when f(x) grows faster than g(x)} \\ \lim_{x\to\infty} \frac{f(x)}{g(x)} &= 0 && \text{when f(x) grows slower than g(x)} \\ \lim_{x\to\infty} \frac{f(x)}{g(x)} &= L && \text{when f(x) grows at the same speed as g(x)} \\ \end{aligned}$$ At a given point $x$ where the functions grow: $e^{x^n} > e^x > x^n > x^\frac{1}{n} > ln(x)$ for $n \in \mathbb{N}$ (higher values imply a faster growth)
Speed of Decaying Functions
$$\begin{aligned} \lim_{x\to\infty} f(x) = 0 && \lim_{x\to\infty} g(x) = 0 \\ \end{aligned}$$ $$\begin{aligned} \lim_{x\to\infty} \frac{f(x)}{g(x)} &= 0 && \text{when f(x) decays faster than g(x)} \\ \lim_{x\to\infty} \frac{f(x)}{g(x)} &= \infty && \text{when f(x) decays slower than g(x)} \\ \lim_{x\to\infty} \frac{f(x)}{g(x)} &= L && \text{when f(x) decays at the same speed as g(x)} \\ \end{aligned}$$ At a given point $x$ where the functions decay: $e^{-x^n} < e^{-x} < x^{-n} < x^{-\frac{1}{n}} < ln(x)^{-1}$ for $n \in \mathbb{N}$ (lower values imply a faster decay)
Equivalent Functions at their Limit
$$\begin{aligned} x &\to \infty \\ x^a + x^b &\sim x^a, a > b \\ e^{ax} + e^{bx} &\sim e^{ax}, a > b \\ ln(x^a) + ln(x^b) &\sim ln(x^a), a > b \\ \\ x &\to 0 \\ e^x - 1 &\sim x \\ ln(1 + x) &\sim x \\ sin(x) &\sim x \\ cos(x) - 1 &\sim -\frac{1}{2} x^2 \\ tan(x) &\sim x \\ \end{aligned}$$
Derivatives
Definition
$$\begin{aligned} f'(x) &= \lim_{\Delta x \to 0} \frac{\Delta f(x)}{\Delta x} \\ &= \lim_{\Delta x \to 0} \frac{f(x + \Delta x) - f(x)}{\Delta x} \end{aligned}$$
Derivatives Algebra
$$\begin{aligned} (kf(x))' &= kf'(x) && \text{ for } k \text{ constant, independent of } x \\ (f(x) + g(x))' &= f'(x) + g'(x) && \\ (f(x) g(x))' &= f'(x)g(x) + f(x)g'(x) \\ (\frac{f(x)}{g(x)})' &= \frac{f'(x)g(x) - f(x)g'(x)}{g^2(x)} \\ f(g(x))' &= f'(g(x))g'(x) \\ (f^{-1}(x))' &= \frac{1}{f'(f^{-1}(x))} \end{aligned}$$
Basic Derivatives
$$\begin{aligned} (k)' &= 0 \\ (x^n)' &= nx^{n-1} \\ (a^x)' &= a^xln(a) \\ (e^x)' &= e^x \\ (ln(x))' &= \frac{1}{x} \\ (log_a(x))' &= \frac{1}{xln(a)} \\ (sin(x))' &= cos(x) \\ (cos(x))' &= -sin(x) \\ (tan(x))' &= \frac{1}{cos^2(x)} \\ (arcsin(x))' &= \frac{1}{\sqrt{1 - x^2}} \\ (arccos(x))' &= \frac{1}{-\sqrt{1 - x^2}} \\ (arctan(x))' &= \frac{1}{\sqrt{1 + x^2}} \\ \end{aligned}$$
L'Hôpital's Rule
$$\begin{aligned} \lim_{x \to c} \frac{f(x)}{g(x)} = \lim_{x \to c} \frac{f'(x)}{g'(x)} \\ \end{aligned}$$
Taylor Expansion
$$\begin{aligned} & f(a) + \frac{f'(a)}{1!}(x-a) + \frac{f''(a)}{2!}(x-a)^2+\frac{f'''(a)}{3!}(x-a)^3 + ... \\ & f(0) + \frac{f'(0)}{1!}x + \frac{f''(0)}{2!}x^2+\frac{f'''(0)}{3!}x^3 + ... \\ \end{aligned}$$