TD 1

Index

Factoring

Exercise 1

By rearranging the original expression, $x$ can be extracted as a common denominator for the first two terms, while $-5$ is also extracted from the other terms. The factor $(x^2-1)$ can then be extracted as a common denominator too. Furthermore, $(x^2-1)$ can be interpreted as $x^2-1^2$ and factorized into $(x+1)(x-1)$ using a common factorization pattern for quadratics. $$\begin{aligned} x^3 - 5x^2 - x + 5 &= x^3 - x - 5x^2 + 5 \\ &= (x^3 - x) - (5x^2 - 5) \\ &= x (x^2-1) - 5 (x^2-1) \\ &= (x-5) (x^2-1) \\ &= (x-5) (x+1) (x-1) \\ \end{aligned}$$

Exercise 3

This expression can be simplified to a quadratic by replacing $x^3$ with another variable, say $w$. By finding the divisors of $-27$, one can notice that $(-27*1=-27)$ and $(-27+1=-26)$, allowing the factorization of this quadratic.

After replacing $w$ back to $x^3$, the remaining cubics of the form $x^3+k^3$ and $x^3-k^3$ can be easily factorized by applying their respective pattern. $$\begin{aligned} x^6-26x^3-27 &= w^2-26x-27 &&\text{with: } w = x^3 \\ &= (w+1)(w-27) \\ &= (x^3+1)(x^3-27) \\ &= (x^3+1^2)(x^3-9^2) \\ &= (x+1)(x^2-x+1)(x^3-3^2) \\ &= (x+1)(x^2-x+1)(x-3)(x^2+3x+9) \\ \end{aligned}$$

Exercise 12

This expression can also be simplified to a quadratic by replacing $x^4$ to $w$. Assuming it has a form of $(ax+p)(bx+q)$, one can test with different divisors of $4$ and $225$ to find the best values for $a,b,p,q$.

Replacing back $w=z^2$ one can repeat the process and factorize the two terms using the same factorization techniques. This can be even done once more after replacing $z=x^2$. $$\begin{aligned} 4x^8 - 61x^4 + 225 &= 4w^2 - 61w + 225 &&\text{with: } w = x^4 \\ &= (4) w^2 + (4 * -9)w + (-25)w + (-9 * -25) \\ &= (4 w^2 + (4 * -9)w) - (25w + 25*(-9)) \\ &= 4w (w - 9) - 25 (w - 9) \\ &= (4w - 25) (w - 9) \\ \\ (4w - 25) (w - 9) &= (4z^2 - 25) (z^2 - 9) &&\text{with: } z = x^2 \\ &= (2z + 5) (2z - 5) (z^2 - 9) \\ &= (2z + 5) (2z - 5) (z + 3) (z - 3) \\ \\ (2z + 5) (2z - 5) (z + 3) (z - 3) &= (2x^2 + 5) (2x^2 - 5) (x^2 + 3) (x^2 - 3) \\ &= (2x^2 + 5) (\sqrt{2}x + \sqrt{5}) (\sqrt{2}x - \sqrt{5}) (x^2 + 3) (x + \sqrt{3}) (x - \sqrt{3}) \\ \end{aligned}$$

Quadratic Formula

For these examples, the quadratic formula is simply applied to the expressions of the form $ax^2 + bx + c = 0$. An equation has no real solution if the value inside the square root (the determinant) is negative, has one solution if it's 0, and has two solutions otherwise (thanks to the plus-minus sign).

Exercise 2

$$\begin{aligned} b^2-4b+4 &= 0 \\ b &= \frac{-(-4) \pm \sqrt{(-4)^2-4(4)}}{2} \\ b &= \frac{4 \pm \sqrt{16-4*4}}{2} \\ b &= \frac{4}{2} \\ b &\in \{2\} \\ \end{aligned}$$

Exercise 7

$$\begin{aligned} 4b^2+8b+7 &= 4 \\ 4b^2+8b+3 &= 0 \\ b &= \frac{-(8) \pm \sqrt{(8)^2-4(4 * 3)}}{2(4)} \\ b &= \frac{-8 \pm \sqrt{64-48}}{8} \\ b &= \frac{-8 \pm \sqrt{16}}{8} \\ b &\in \{ -\frac{1}{2}, -\frac{3}{2} \} \\ \end{aligned}$$

Radical Equations

These can be solved by squaring both sides of the equation, then solving the resulting polynomial. However, one must keep in mind the constraints given by the initial expression: square roots must take positive (or 0) values as input and return positive (or 0) values as output. These must be checked after solving the polynomial and invalid results discarded.

Exercise 1

$$\begin{aligned} \sqrt{110 - n} &= n \\ n^2 + n - 110 &= 0 &&\text{with: } 0 \leq n \leq 110 \\ n^2 + 11n - 10n - 110 &= 0 \\ (n + 11) (n - 10) &= 0 && n \in\{10\} \end{aligned}$$

Exercise 13

$$\begin{aligned} \sqrt{-16 + 10a} &= a \\ a^2 - 10a + 16 &= 0 &&\text{with: } a \geq \frac{5}{8} \\ a^2 - 2a - 8a + 16 &= 0 \\ (a - 2) (a - 8) &= 0 && a \in \{2, 8\} \\ \end{aligned}$$

Exercise 14

$$\begin{aligned} r &= \sqrt{-1 -2r} \\ r^2 + 2r + 1 &= 0 && \text{r has no real solution} \end{aligned}$$

Absolute Value Equations

For these equations, one must consider that absolute values have the same output whether its input is positive or negative. Therefore, one can remove the absolute value and consider two possible equations: one where the term with the absolute value is kept the same, and another where the input of the absolute value has its sign inverted.

Exercise 1

$$\begin{aligned} \mid 6m \mid &= 42 \left \{ \begin{align*} 6m &= 42 \rightarrow m = 7 \\ -6m &= 42 \rightarrow m = -7 \\ \end{align*} \right . \end{aligned}$$

Exercise 17

$$\begin{aligned} \left | \frac{-9+v}{8} \right | &= 3 \left \{ \begin{align*} -9 + v &= 24 \rightarrow v = 33 \\ 9 - v &= 24 \rightarrow v = -15 \\ \end{align*} \right . \end{aligned}$$

Exercise 18

$$\begin{aligned} -10 \left | v + 2 \right | &= -70 \left \{ \begin{align*} v+2 &= 7 \rightarrow v = 5 \\ -v-2 &= 7 \rightarrow v = -9 \\ \end{align*} \right . \end{aligned}$$

Rational Equations

These equations can be solved by multiplying both sides by the same terms until no fractions are present, then solving for the resulting polynomial. One must keep in mind the constraints given by the original form of the equation: solutions that make a denominator be equal to 0 are to be excluded from the solution set.

Exercise 1

$$\begin{aligned} \frac{k+4}{4} + \frac{k-1}{4} &= \frac{k+4}{4k} &&\text{with: } k \neq 0 \\ (4k)\frac{k+4}{4} + (4k)\frac{k-1}{4} - (4k)\frac{k+4}{4k} &= 0(4k) \\ k(k + 4) + k(k - 1) - (k+4) &= 0 \\ k^2 + 4k + k^2 - k - k - 4 &= 0 \\ 2k^2 +2k - 4 &= 0 \\ k^2 + k - 2 &= 0 \\ (k+2)(k-1) &= 0 && k \in \{ -2, 1 \} \\ \end{aligned}$$

Exercise 2

$$\begin{aligned} \frac{1}{2m^2} &= \frac{1}{m} - \frac{1}{2} &&\text{with: } m \neq 0 \\ 1 &= \frac{2m^2}{m} - \frac{2m^2}{2} \\ &= 2m - m^2 - 1 = 0 \\ &= m^2 - 2m - 1 \\ &= (m-1)^2 && m \in \{ 1 \} \\ \end{aligned}$$

Exercise 9

$$\begin{aligned} \frac{1}{r+3} &= \frac{r+4}{r-2} + \frac{6}{r-2} &&\text{with: } r \notin \{ -3, 2 \} \\ r-2 &= (r+3)(r+4)+(r+3)6 \\ 0 &= r^2+7r+12+6r+18-r+2 \\ &= r^2+12r+32 \\ &= (r+4)(r+8) && r \in \{ -8, -4 \} \end{aligned}$$

Analyzing and Solving Polynomial Equations

The number of complex roots of a polynomial is given by the highest exponential term. The possible number of real roots for a polynomial of degree $n$ is $0,2,4,...,n$ if $n$ is even or $1,3,5,...,n$ if $n$ is odd. The number of imaginary roots is just the number of complex roots minus the number of real roots.

The number of positive real roots is obtained using Descartes' rule of signs for the polynomial $f(x)$, which consists of counting the number of sign changes in the expression (with the polynomial terms sorted in descending order). The number of negative real is similarly obtained, this time considering the sign changes of $f(-x)$.

The possible rational roots are the divisors of the constant term of the polynomial (i.e. $kx^0$). The roots of the polynomials are values of $x$ where $f(x) = 0$.

Exercise 1

Obtaining the roots

$$\begin{aligned} 0 &= x^4-5x^2-36 \\ &= (x^2+4)(x^2-9) \\ &= (x+2i)(x-2i)(x+3)(x-3) \\ \\ x &\in \{ -3, 3, -2i, 2i \} \\ \end{aligned}$$

Problems (Systems of Equations)

Exercise 7

When confronted with questions such as $$ \text{How many students can a van carry}? \\ \text{How many students can a bus carry}?, $$ it is useful to rewrite them as statements involving well defined variables and units, in this case: $$ \text{A } van \text{ has a capacity of } v * \frac{student}{van}\\ \text{A } bus \text{ has a capacity of } b * \frac{student}{bus}, $$ where $van$, $bus$ and $student$ are units of measure, and $v$ and $b$ are incognita values. This abstraction then allows to extract other pieces of information from the problem, for example the phrase $$ \text{High School B rented and filled 4 vans and 1 bus with 54 students} $$ can be rewritten (and simplified) as: $$\begin{aligned} 4 van * v * \frac{student}{van} + 1 bus * b * \frac{student}{bus} &= 54 student \\ 4v * student + 1b * student &= 54 student \\ 4v + b &= 54 \\ \end{aligned}$$ In this example, the problem can be converted to a system of equations and solved accordingly. $$\left \{ \begin{align*} 8v+8b&=240 \\ 4v+b&=54 \\ \end{align*} \right . $$ $$\begin{aligned} 8v+8b-240 &= 8v+2b-108 \\ 6b &= 132 \\ b &= 22 \\ \\ 4v+22&=54 \\ 4v &= 32 \\ v &= 8 \\ \end{aligned}$$

Exercise 9

With experience, problems can be directly rewritten to equations without including "redundant" units. However, a good understanding of the concept of units is crucial for most physics formulas and biological models, specially when the models get more convoluted. Units might seem unnecesary for these toy examples, but it's greatly adviced to take them into account when dealing with real life mathematical problems. $$\left \{ \begin{align*} 3s+9c &= 75 \\ 8s+5c &= 67 \\ \end{align*} \right . $$ $$\begin{aligned} 8(3s + 9c - 75) &= 3(8s+5c-67) \\ 24s+72c-600 &= 24s-15c-201 \\ 57c &= 399 \\ c &= 7 \\ \\ 3s + 9(7) &= 75 \\ 3s &= 75-63 \\ s &= \frac{12}{3} \\ s &= 4 \\ \end{aligned}$$

Multistep Inequalities

Inequalities can be, for the most part, treated and solved as equations. However, one must be very careful when multiplying both sides of the inequality with a negative number, as this reverts the inequality. For example, given $a < b$, if both sides are multiplied by $-1$, the inequality becomes $-a > -b$ (can also be written as $-b < -a$).

When plotting an inequality such as $x > k$ in the number line, a point must first be drawn in $k$. Then, one can highlight a line going either towards minus (if the inequality is $x < k$) or plus (if the inequality is $x > k$) infinity. The dot at $x = k$ is filled for the inequalities $x >= k$ and $x <= k$, and empty for $x > k$ and $x < k$.

Exercise 1

$$\begin{aligned} 3 &< -5n + 2n \\ 3 &< -3n \\ 1 &< -n \\ n &< -1 \\ \end{aligned}$$

figures/td1-ineq-1.png

Exercise 3

$$\begin{aligned} -p-4p &> -10 \\ -5p &> -10 \\ -p &> -2 \\ p &< 2 \\ \end{aligned}$$

figures/td1-ineq-3.png

Exercise 8

$$\begin{aligned} -138 &\geq -6(6b - 7) \\ -138 &\geq -36b + 42 \\ -138-42 &\geq -36b \\ -180 &\geq -36b \\ -5 &\geq -b \\ b &\geq 5 \\ \end{aligned}$$

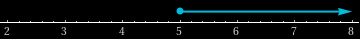
figures/td1-ineq-8.png

Quadratic Inequalities

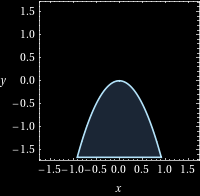
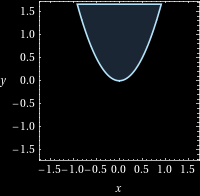
When plotting an inequality such as $y > f(x)$ in a cartesian plane, first plot the line described by $y = f(x)$. Then, one can shade either the area above (if the inequality is $y > f(x)$) or below (if the inequality is $y < f(x)$) this line. The line $y = f(x)$ must be included if the inequality is $y >= f(x)$ or $y <= f(x)$, otherwise it should be excluded (usually represented with a dotted line).

Exercise 1

$$\begin{aligned} y &>= 2x^2 \end{aligned}$$

figures/td1-ineq_quad-1.png

Exercise 4

$$\begin{aligned} y < -2x^2 \end{aligned}$$

figures/td1-ineq_quad-4.png